Contenidos

3. Análisis de una trayectoria a través de un vídeo con Tracker

El programa Tracker, del proyecto Open Source Physics, es una herramienta de análisis de vídeos en formato abierto que permite obtener los datos de una trayectoria 𝒓(𝑡), 𝒗(𝑡) y 𝒂(𝑡) de manera sencilla y compararlos con modelos analíticos y dinámicos, sin necesidad de conocimientos previos de programación. Este programa está integrado en el proyecto ComPADRE de la American Association of Physics Teachers para compartir materiales didácticos en abierto para la enseñanza de la Física a nivel de educación Secundaria y Universidad.

El material necesario para hacer un experimento de análisis de video es, simplemente, una cámara de video (la de un Smartphone, por ejemplo) y un PC con el software Tracker instalado. Veamos ahora como realizar el análisis de una trayectoria (se puede descargar un guion detallado con cada uno de los comandos del proceso paso a paso o ver un tutorial preparado por alumnos de primero de grado de Física en la web del proyecto SmartFis.)

3.1 Realización de un vídeo: el punto de partida es el video de una trayectoria plana (en 2D) que permita demostrar algún problema físico interesante: caída por un plano  inclinado, tiro parabólico o con resistencia al aire, movimiento en un fluido, choques elásticos o inelásticos, movimiento en videojuegos, etc. Para evitar distorsiones conviene que la cámara esté fija, situada a una cierta distancia del plano de la trayectoria y dibujar una marca pequeña brillante que sirva para definir el punto P de la partícula en cada fotograma. También se debe incluir un objeto de tamaño conocido en el mismo plano de la trayectoria. Tracker admite los formatos de video habituales que proporciona un Smartphone (mp4, mov, etc).

3.2 Importar el vídeo y calibrar las escalas de tiempo y longitud: el primer paso al importar el video es definir la escala de tiempo (que dependerá de la velocidad de grabación en frames per second (fps) y el instante inicial t0. A continuación se empleará la opción “Vara de calibración” para introducir la equivalencia pixel/metro utilizando un objeto de dimensiones conocidas que se haya incluido en la imagen. Es un buen momento para introducir de forma práctica conceptos como la orientación de los ejes respecto al marco de la imagen.

3.3 Definir el sistema de referencia: se pasa ahora a definir el sistema de referencia, tanto el origen de coordenadas como la orientación de los ejes respecto al marco de la imagen.

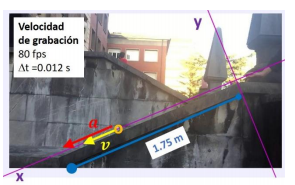
3.4 Definir la trayectoria de la partícula. Este es el punto más importante del análisis: crear una tabla de valores una tabla de valores de posición en función del tiempo (t_i, x_i, y_i) a partir de la posición de la partícula en cada fotograma. Se puede hacer de modo manual, marcando con el ratón en cada fotograma o de modo automático con la opción Autotracker. Esta segunda opción disminuye el ruido en las derivadas numéricas pero requiere que la forma de la partícula esté muy bien definida en cada fotograma.

3.5 Obtener los vectores 𝒗(𝑡) y 𝒂(𝑡). Tracker calcula de forma automática los vectores velocidad y aceleración a partir de la derivada numérica de los datos de trayectoria. Permite también realizar distintas gráficas de los parámetros de la trayectoria en función del tiempo o la posición y exportar las tablas de datos si se quieren tratar con un software diferente.

3.6 Definir un modelo analítico de 𝒓(𝑡). Por último, es posible definir modelos teóricos y hacer una comparación directa con la trayectoria experimental. Para movimientos sencillos se puede usar un “Modelo analítico de la partícula” e introducir las expresiones x(t) e y(t) previstas por la teoría e ir variando los parámetros característicos hasta ajustar la trayectoria experimental. Por ejemplo, para el movimiento rectilíneo descrito en la figura 3, se puede partir de la ecuación x(t) = x₀+v₀t+½a₀t² e ir variando x_{0 ,} v_{0 y} a_{0 .}

3.7 Definir un modelo dinámico de la partícula. Una de las opciones más interesantes de Tracker es la posibilidad de introducir directamente las ecuaciones de la fuerza en coordenadas cartesianas o polares y realizar la integración numérica del movimiento a partir de las condiciones iniciales de posición y velocidad (ec. (3)). Esto amplía mucho el tipo de problemas que se pueden tratar de forma cuantitativa a casos en los que no se pueda definir la ecuación analítica de la trayectoria, o a la docencia de alumnos que están todavía iniciándose en el Cálculo Diferencial e Integral y no están familiarizados con las ecuaciones diferenciales.